Explaining well is foundational to teaching well

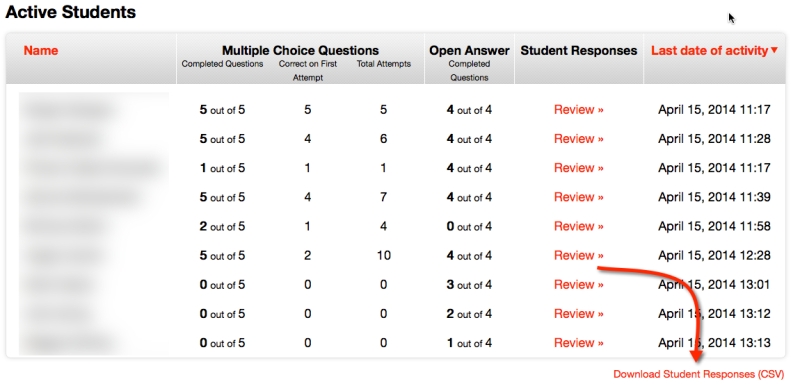
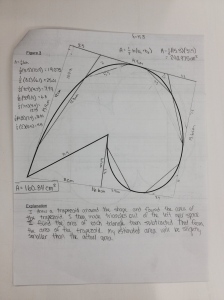
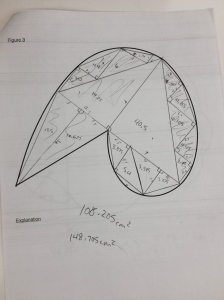
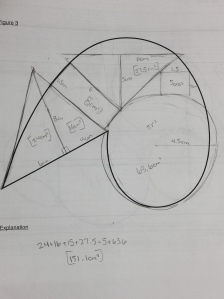
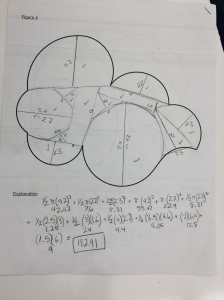
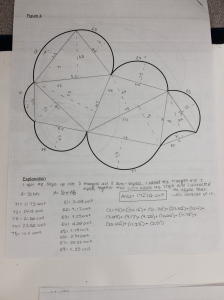
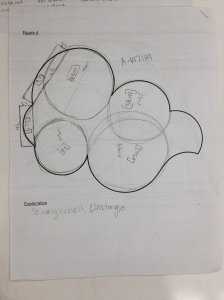
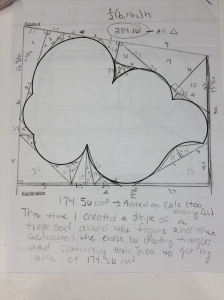
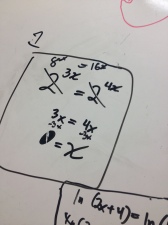
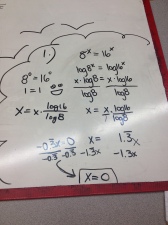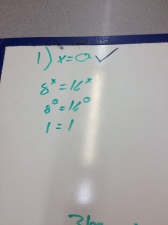The ability to explain things clearly is a necessary condition for being a good math teacher. 

Many conversations in some circles are around creating activities that help students construct knowledge and understand concepts more deeply. This is great! 

But young teachers need to know that explaining concepts clearly is foundational to those activities. 

Not that I’m in a position to do it much, but when I talk to young teachers I tell them to teach primarily with direct instruction/guided practice/independent practice/formative assessment their first couple of years. Focus on getting the content solidified in your own mind and explaining it well. Once you have it vividly in your own mind you can then develop (or bring in) activities and more advanced pedagogy. 

There is a real risk that leaning into those kinds of activities without the ability to explain it well will result in students being confused and feeling lost – consistently. This has implications for classroom management, culture, and ultimately student learning. All of that can be compounded by other factors, such as the age of your students and their mathematical abilities when they come to you. 

I think we sometimes forget the role that explaining plays in our own learning. Imagine looking up a youtube video for how to change a headlight and the video starts off with “I want you to take some time and explore the area around the light bulb and consider how you might change the light bulb. Push and pull on different things. What questions do you have about the different pieces of the headlight casing?” 

You’d move on to the next video. 

“But,” I hear you say, “learning mathematics isn’t like learning how to change a headlight. We want students to understand the mathematics deeply, not just to be able to perform the actions!” 

I’m with you. Let’s pull back and assume you’re trying to teach about the entire electric system of the car. Teaching explicitly (by which I don’t mean purely lecturing, but balancing lecture with guided practice and independent practice) about the electrical system will allow you to understand the entire system more deeply. 

From that depth of understanding you will be able to generate more targeted and effective inquiry activities. Most importantly, you’ll have a knowledge base from which you can pull more effective explanations and questions. As you deepen your knowledge you will learn what concepts are best taught explicitly and which are best taught through inquiry activities. 

And it’s not as if you are giving your students a bad education in the process. I don’t want you to think this is merely about suspending good teaching so you can understand algebra II better. Students will learn if you’re teaching explicitly well. Maybe not maximally, but it’s certainly not an exercise in suspending student learning for teacher depth of knowledge.  

The best teachers are pedagogical ninjas, with strong foundational principles coupled with the ability to respond and adjust in the moment. When you graduate college with a math degree you might be very strong mathematically. But just as being strong is only part – and probably not the most important part – of being a good martial artist, the strength you get from a math degree does not translate directly into being a great teacher. 

Get good at explaining things clearly so students understand that you’re competent and trust that you can teach them well. This will help you manage your classroom, especially early on in your career before you’ve developed a reputation. It will give you richer knowledge of your content. Then gradually bring in inquiry activities in targeted ways. To bring in one more analogy, you can’t build a nice house on a weak foundation. It doesn’t matter how nice the landscaping looks if the house is on a slant and basement fills with water every time it rains. Even if the landscaping is what people see when they drive by – and your favorite thing to talk about. 

I have a couple of questions about “Social Justice Math”

I have a couple concerns regarding “Social Justice Math” that I don’t think I’ve seen addressed. (If they have been, please let me know.)

From what I’ve read SJM is billed as a way to bring real world problems into the classroom with a “justice” lens. Problems related to climate change, economic inequality, racial equity, etc., would be used in class as frameworks for learning different math concepts. (Read more on that here.) In fact, it sounds a lot like Project Based Learning but with a more refined list of suggested issues to study.

The first concern I have is that, like it or not, “Social Justice” is associated with the political left.

Do those advocating for SJM openly say this is a political slant on mathematics and embrace it as such? (Let’s call this “motivation A”.)

Or do they argue they’re talking about social justice (fairness to people in general, without the political connotation) and not Social Justice? (Let’s call this “motivation B”.)

In the former case I’d have real concerns if I was conservative minded person and my child was in that class (or independently/liberal minded and concerned about one political viewpoint seeping into mathematics curriculum). In the latter case the perception will still almost certainly be taken as a leftward spin on math, again because “social justice” is attached to the political left.

The second concern I have is, what exactly is the “social justice” aspect of the math. Is it simply the selection of the topics chosen? Or is it in the conclusions that come from the students’ analysis? Will the teacher point out that social problems are complicated and that both the left and the right have something to say about their causes and solutions?

I can imagine a teacher trying to present these problems in an unbiased fashion and letting students arrive at a variety of remedies to the problems (motivation B folks). But I would bet money that many teachers implementing SJM will be pushing students to arrive at solutions from the political left (motivation A folks).

If they weren’t, then why call it “social justice” math? Why not call it “real world mathematics” or some other less politically charged title that still acknowledges you’ll be analyzing problems that humanity faces? (Again, this seems a lot like a political form of Project Based Learning.)

I fear “Social Justice Mathematics” is the title because they don’t want students to learn to take a dispassionate approach to the problems. They want students to take a certain, Social Justice approved, approach to analyzing the problems. If this is the case then I think we’d be right to push back against SJM, and if it isn’t the case then SJM will face a branding issue for the foreseeable future.

Are my concerns justified or am I way off base? I’d love to discuss it in the comments.

Three Arguments for a Mathematical “SSR”

I’m sure that at some point in your life you’ve either heard of or participated in sustained silent reading in school. The idea is that students simply spend a set amount of time reading anything they enjoy for an extended period of time. I remember doing it in middle and elementary school. Every English student in the high school in which I currently teach does it as well. In fact, since it’s implementation there has been a notable increase in our reading scores. This got me thinking….what would the mathematical equivalent of this look like and would it be valuable?

Choice

I think it might have a few components. One of the main premises of SSR is you get to choose what you read. In the realm of mathematics I don’t doubt that many students would need guidance in this area for a couple of reasons. First, many students see mathematics through the lens of their math books and previous math books that led to their current math book. This means that they are sheltered from a lot of math they might find interesting. Second many don’t know what doing math is like. For instance, have a look at this video by Vi Hart (who has one of my favorite Youtube Channels) in which by doodling she makes parabolas incredibly interesting. This is an exceptional example of where simply playing with mathematics can take you. Now, I understand that her mathematical background allowed her to draw and discuss parts of the video that would be over many student’s heads. The point is that there are many access points to mathematics that are both playful and creative. The teacher would have to front load some of the explanation for what constitutes mathematics, to broaden their horizons.

Being able to choose the mathematics students work on gives them some ownership of the content, even if it’s only for a small part of the week. Math catches a bad rep. Even certain students in my AP calculus would hesitate to brag about their love of math and a number of them don’t like math. I’m not contending that after implementing some sort of mathematical SSR that everyone will be running around jumping up and down about how great math is. I’m simply contending that if students view of mathematics broadens into something they think is enjoyable, the subject in general might be viewed in a better light. I would also hope that there would be a “spillover” effect in math class. This would stem from the notion that, although “what you’re telling me now isn’t particularly interesting, I can see that there are parts of this subject that are.” The goal would be that students would be (even slightly) more motivated to learn other mathematics.

Thinking

I constantly preach to my students that if you want to get better at something you have to work at it. No one wakes up one morning with the ability to shoot three pointers at 60%. Likewise, no one wakes up one morning with the ability to do and fully comprehend integral calculus. To this end, if we can get students thinking mathematically for a short period each week I believe that ultimately students would become better mathematical thinkers and problem solvers. Two of the critical components to the success of this is that a) students have enough time each week to make it worthwhile and b) students engage in activities that make them reason and use their logical thinking skills.

Focus

I don’t think I’m alone when I observe that many students in my class are trying to do math with a computer sitting next to them, lighting up every 15 seconds. This makes any kind of extended focus and concentration difficult. How are students supposed to “make sense of problems and persevere in solving them” if their phone is constantly distracting them from what their work? To this end a mathematical SSR would be phone/distraction free. I’m not sure if English classrooms implement it this way, but I imagine they do. One of the goals of this would be that students get better at concentrating on problems for longer than a minute or two. My hope is that students would begin to see value in distraction free work. They might even increase their ability to focus.

Nuts and Bolts

A few things remain to be worked out. For instance, what are the guidelines for something mathematical. Vi Hart spent a bunch of time drawing parabolas but the result was much more mathematical than if most of my students did the same. Here’s a list of activities that, I think, would be fit this time nicely.

• Logic Puzzles
• Creating Desmos Art
• Sudoku, Kakuro, etc.
• Reading and playing games on Math Munch
• Something they find interesting from (gasp) the textbook
• Watching Youtube videos from approved Youtube channels (I’m not sold on this one…)
• Maker Stuff (Little Bits, Arduino, etc.)
• Logic Games
• Games (Chess, Guillotine, etc.)
• Coding
• Others (If you shoot me ideas then I’d love to add them to the list…)

This time would be explicitly not for remediation. I can think of no worse way for a student to spend this time than being forced to do math they don’t find interesting and are already struggling with. I can see the temptation for a teacher to fill this chunk of time with remediation but that completely misses the point.

Results

I have to believe that the end result would be better mathematical understanding in general. I also think that (another gasp) test scores would go up as a result. Many standardized test questions test reasoning more than given math skills anyway. I have no research to prove this, I just think that if students do more mathematical thinking, their math skills will improve. And to be quite honest, if the results are simply more students improving their reasoning ability and gaining a new appreciation for mathematics then I’d deem it a success.

On a final note, I think it’s important that the teacher does this with the students. This models what is expected and gives the teacher some time to explore the subject that they love. It would contribute to a culture of mathematics in the classroom and sends a message to the students that this time is valuable to the teacher as well.

This is just an idea that’s been pinging around my head for several months and I’m finally getting it out. I’d really love to hear feedback on this, including but not limited to “this idea sucks because…”.

This Quote From a Student Made Me Smile

“Additionally, Mr. Cresswell didn’t hold us in a right-wrong mindset while working on the problem – we were focused more on discussion.“

Making Review Less boring

We are closing out our probability unit and instead of giving my students 30 problems of review to complete in class I designed a “station” activity. The station format idea actually came from a couple colleagues of mine, and it really helps to get kids up and moving. Also, as the title implies, makes review a little less boring.

I wanted to put a creative twist on this so I came up with the following station activity. There entire activity is self contained, meaning that you don’t need our textbook to use it as I designed the problems. You should be able to run it as is, or modify/improve it as you like.

Also, Ted-Ed deserves it’s own paragraph for it’s awesomeness. Now that I’ve actually gone through and used it to flip a lesson (or part of an activity really), I’m really excited about using it next year in my flipped classroom (or even my non-flipped classes)!

In addition, my good friend and colleague Eric Beckman, recorded the activity for me. Here is my reflection, and the activity resources:

Station Reflection

Stations 1 & 2: In these stations students were asked to watch two Ted-Ed lessons the night before (Station 1, station 2). I then used some of the provided questions, and created my own, for them to answer after watching the lessons. I loved that I get great data on their responses and that students can participate in discussions. I can review all student responses, both open ended and multiple choice, as you can see in the screen shot below. I can also give feedback to the open ended questions, and students will be notified when I give that feedback. You can also download all the responses as a CSV file. The discussions centered around the problems seemed really thoughtful, so I was happy with that. The videos also provide a different perspective on the concepts for the students, which I think was helpful for some.

This did however take them more time than I anticipated. I had one student from each group create an account, which took time, and some of the questions were tougher for them then I anticipated. Next time I will have them set up with Ted-Ed accounts when they come to class, and will also likely reduce the number of problems they have to answer. Because some groups took a while, some groups didn’t complete all the stations.

Stations 3-5: These were the basic probability problems. Students did well on these to varying degrees. I could’ve given these problems all as one station, but breaking it into multiple stations broke it up for that students. Sometimes simple things like that make math more approachable for students. It’s also important to have the key available for students so they can get instant feedback if I’m not available.

Station 6: This station asked students to solve two problems and then create two short video lessons using my iPad to explain their solution. Every time I do this I get mixed results, but the good results outweigh the bad. The downside is that students really don’t like doing it so some push back a bit. However, it forces students to take their understanding to the next level. They will learn it better if they are forced to teach it. It makes them take an extra step in understanding, as they don’t want to explain it incorrectly on record, or mess up and have to re record it. I need to do more of this, as the students that really try get a lot out of creating short lessons explaining concepts.

Stations 7 & 8: More practice problems, similar to stations 3-5.

Activity Resources

Station Packet (PDF)                    Station Packet (Pages)                Station Packet (Word) – I make no promises about formatting….

Station Packet Answer Key

Ted-Ed Lesson for Station 1        Ted-Ed Lesson for Station 2        (These are editable, so feel free tow tweak to fit your needs)

 

Finding Areas in AP Calculus (without talking about calculus)

I’ve probably mentioned this elsewhere in my blog but one of my goals this year is to introduce each major topic using an exploration or by allowing students to “play” with the math. In that theme I considered different ways to introduce the topic of finding areas under curves in calculus.

I felt like each time I’ve either learned it or taught it, this idea is just dropped on the student. It’s actually a profound idea and technique that we use to find these areas. I wanted to solidify the idea that, by using areas of “normal” shapes, we can get decent estimations of areas of abnormal. In addition, I wanted students to see that the more shapes you use and the smaller the shapes the more accurate your measurement of the area. To do this, I gave students four shapes that had varying degrees of “squigglyness”. They had to use a ruler and formulas they already new to get measurements for the areas as accurate as possible. They also had to explain their method for finding the areas.

The activity went really well. I found a lot of value in not helping at all. Students asked “what’s the best way to find the area of this?” and I said “I don’t know.” I made sure to point out that there was no correct method for finding the area and many students used different methods. We finished by comparing all the areas in this google doc and discussing who had the most accurate method. What I loved about the activity is that students engaged in problems with no obvious answers that required them to think critically. It was then a natural segue into this activity, where we look at finding areas under curves.

Below are some samples of the students’ work. I definitely enjoyed the different methods and thought processes that students demonstrated. As usual, any feedback you can give would be much appreciated!

  

Multiple Methods for a Simple Problem

For each video I have students watch I ask them, among other things, to submit one question they have after watching the video. After a student watched the “Solving Logarithmic and Exponential Equations” video, he submitted the following question.

How would you solve 8^x = 16^x ?

The following day I used this question in our WSQ chat over the video. What appeared to be a simple problem revealed some interesting solutions. I’ve provided the main types of solutions that I found.

I anticipated the second method from most students but only two of the five groups approached it that way. All methods are valid and what I really liked is that not only were they different methods but also different thought processes that led to the method/solution.

I would love to hear your feedback or observations that you have seen in your class!

I want to assess my students on more than just skills… I think

This is my second year of teaching AP calculus. Last year I felt like my students weren’t getting a full understanding of the conceptual underpinnings of calculus. This year, I’ve been taking a little bit more time with concepts, Implementing more activities that aren’t skills practice, but ask students to dig deeper into the math. I’m trying very hard to get students to talk about the math more. (See my last post.) Also, my students are doing metacognitive journaling every week via a blog. This is another technique I’m using to try to get kids to think deeper about the concepts. In the journaling and in the conversations it seems like I’m seeing good conceptual understanding. However, when I gave the most recent quiz I saw that my students seem to be lacking in applying those concepts to new situations. Let me explain more.

The problems that students practiced over and over, the skills problems, seemed to go pretty well. The problems that ask students to explain concepts directly, also seemed to go pretty well. However, there were some skills type problems that were really asking students to take the concepts and apply them in a slightly different way. My thoughts in writing those problems were that students would have the tools they needed to solve them, they just needed to pull the right tools out of the box and apply them. Either my students didn’t know which tools to use, or they weren’t entirely sure of what the tools they had were used for.

There seems to be a disconnect. My students can practice something over and over and over again and replicate those processes on the test. (Maybe this isn’t surprising.) My students seem to be able to grab on to conceptual underpinnings and explain them. However they struggle to apply the concepts in new situations. I’m still not entirely sure of how to bridge that gap. How do I put students in a position to be successful on those types of problems?

If You Can’t Do it by Yourself… Crowdsource It! (How I handle Questions over assignments in AP Calculus)

Last year my AP calculus class ran like many math classes. There was a lecture and maybe an exploration or lab, then some independent practice time, and whatever students didn’t get done they took home as homework. Then the following day I would take questions from the class and answer as many as I could before the lesson had to begin.

Every year (or trimester for that matter) I agonize over how I should structure daily work and the grading of that work in my class. This summer was no different, especially in calculus. I wanted to strike a balance between gaining formative knowledge for me and allowing students enough independent practice, all while trying to incorporate more collaboration.

One of my professors in college took an interesting approach to assessing homework. Each day we would arrive to class and fill out our part of a spreadsheet. For each homework problem we would answer the question “Do you feel confident enough in your answer to present it to the class?” He would then select a couple students to present their solutions to certain problems to the class. This method was certainly different, and had a number of problems associated with it (for instance, I have no idea how he established a grade for us using this method) but I certainly thought the question that he was asking us was interesting.

So, in the middle of July as I am writing idea webs on a whiteboard in the bedroom my wife comes in and gives me the following idea. She said “Why don’t you ask the students that same question but, ask them before they come to class. Then when they get the class, have them teach each other in small groups.” From there, I looked at how technology could help me aggregate this “confidence data” And I worked out the details of how this would look in class. (You can see the flowchart that I made for my students here.)

It basically works like this: students have time at the end of each hour to work on their assignment. Once they finish their assignment they fill out a Google form that looks like this: This gives me a big picture of how the assignment went as well as which specific problems were most difficult for students. When students get to class each pod is assigned a problem (Click for diagram). For instance, Pod 1 might be assigned problem #52. Then, for 10 to 15 minutes students are to go to whichever pod is assigned the problem(s) they struggled with, and work on that problem. If students fully understood the assignment they are to go around and help other students with the assignment. Everyone has something to do. (I should also note that I have several “mega” whiteboards that are laid out on each pod when students come to class.)

Let Students Explore and Collaborate (week 1)

We had a great first week! This is my third year of teaching and this is by far the most excited I have been for the rest of the school year. Steve Kelly and I tried a few new things last year in pre calculus and calculus that we didn’t care for, so we revamped the prerequisite units in pre calculus and calculus (again). I have provided links to both documents.

In pre calculus we created a packet for the students with 5 activities. The first asked them to make a piece of art using Geogebra or Desmos and then upload that art to their blog. This had kids a little confused and some weren’t really sure how to begin. It helped that I gave them an example of art I made with Desmos. I don’t think this was a terrible situation as I think it gave activity 5 more meaning and the final works of art were much better. The intermediate activities build on one another And are designed to lead the student to an understanding of the families of functions and transformations. This should be review, but quite often the families of functions are taught in isolation and students lose the big picture. This is especially true for the understanding of how any function is moved left, or right or up-and-down, or reflected. Our objective was that by the end of the packet students would be able to create a better piece of art and understand why their art looked the way that it did.

In calculus, Steve and I sat down together and determined the concepts in mathematics that are most important to be successful in calculus. These included skills like understanding composition of functions, graphical reasoning skills, algebraic manipulation skills, domain and range analysis, and a myriad of other skills. This was successful, as students were given an opportunity to refresh their brains, get back into math mode, and collaborate.

Both of these activities, although in structure were quite different, set the stage for a year full of collaboration and communication.

(I will post some the artwork in another post.)

Calculus packet

Precalculus Packet